Important Measures of Transport Networks
Network analysis is an
important aspect of transport geography because it involves the description of
the disposition of nodes and their relationships and line or linkage of distribution.
It gives measures of accessibility and connectivity and also allows comparisons
to be made between regional networks within a country and between other
countries.
As Fitzgerald (1974) has
said, variations in the characteristics of networks may be considered to
reflect certain spatial aspects of the socio-economic system.
The details of important
measures of transport networks are given here for proper understanding and
application of these measures for:
(i) The
connectivity of networks;
(ii) The centrality within networks;
(iii) The spread and diameter of networks; and
(iv) Detours.
1.
Connectivity and its Measurement:
“The connectivity of a network may be defined as the
degree of completeness of the links between nodes” (Robinson and Bamford,
1978). When a network is abstracted as a set of edges that are related to set
of vertices (nodes), a fundamental question is the degree to which all pairs of
vertices are interconnected.
“The degree of connection between all vertices is defined
as the connectivity of the networks” (Taaffe and Gauthier, 1973). The greater
the degree of connectivity within a transportation network, the more efficient
with that system be. Kansky (1963) has studied the structure of transportation
networks, developed several descriptive indices for measuring the connectivity
of networks, i.e., beta, gamma, alpha indices and cyclomatic number.
Beta Index
(β):
The beta index is a very simple measure of connectivity,
which can be found by dividing the total number of arcs in a network by the
total number of nodes, thus:
β = arcs/ nodes
The beta index ranges from 0.0 for networks, which
consist just of nodes with no arcs, through 1.0 and greater where networks are
well connected.
Some characteristics of P
index are:
(i) β value for tree types of structures and disconnected
networks would always be less than 1. It would take zero values when there are
no edges in the network
(ii) β value for any network structure with one circuit
would always be equal to 1.
(iii) β value exceeds 1 for a complicated network
structure having more than one circuit.
Alpha
Index (α):
One of the most useful measures of the connectivity of a
network, particularly a fairly complex network, is the alpha index (α). The
alpha index (α) for a non-planar graph may thus be defined as:
α= actual circuit/ maximum circuits
Or
α= e-ν+1/ 2ν-5
The alpha index gives the range values from 0 to 1 that
is from 0 to 100 per cent. If the index is multiplied by 100 this will convert
it into percentage, thereby giving the number of fundamental circuits as a
percentage of the maximum number possible. The higher the index, the greater is
the degree of connectivity in the network.
Figure 4.4 shows two networks having the same number of
vertices but different structures. It may be observed that the maximum number
of possible circuits in the two networks is only 5, that is, (2v – 5). In the
case of the first network, the number of actual circuits is zero and hence it
takes the minimum value that is = 0. In the second network, only two circuits
have been formed and hence 2/5 = 0.40.
Gamma
Index (ү):
The gamma index (y) is a ratio between the observed
number of edges and vertices of a given transportation network. For a
non-planar graph, the gamma index has been defined as:
ү=e/3(v – 2)
Stated in other words, y is a ratio of the observed
number of edges (e) to the maximum number of edges in as planar graph. The
connectivity as measured by y index varies from a set of nodes having no
interconnection to the one in which every node has an edge connected to every
other node in the graph.
The connectivity of the network is evaluated in terms of
the degree to which the network deviates from an unconnected graph and
approximates a maximally connected one. The numerical range for the gamma index
is between 0 and 1. This measure may be written in the form of percentage and
would thus range from 0 to 100. Figure 4.5 shows the maximal connectivity. It
is evident from the figure that for a planar graph, the addition of each vertex
to the system increases the maximum number of edges by three. This proposition
is true for any planar network with more than two vertices.
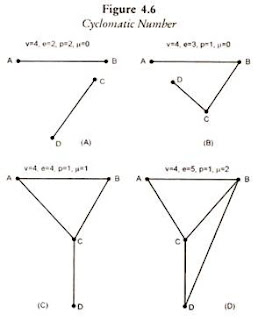
Cyclomatic
Number:
Cyclomatic number is a different way of measuring connectivity.
This is based upon the condition that as soon as a connected network has enough
arcs or links to form a tree, then any additional arcs will result in the
formation of circuits. Thus, the number of circuits in a connected network
equals the total number of arcs minus the number of arcs required to form a
tree, i.e., one less than the nodes or vertices. It may be written as:
Cyclomatic number = a – (n – 1)
Or
a – n + 1
Where a equals the number of arcs and n the number of
nodes. This formula applies to a connected graph, where there happens to be two
or more sub-graphs. Then, the formula for cyclomatic number is:
a – n + x
where x equals the number of subgraphs. This has also
been expressed as:
Cyclomatic number (µ) = e – v + p
e = number of edges or arcs
v = number of vertices or nodes
p = number of non-connected
The relationship of the cyclomatic number with the
network structure has been examined through Figure 4.6. Let us consider a
network consisting of four nodes A, B, C, and D.
In a disconnected position or a tree type graph it has a
cyclomatic number of 0, whereas as the graph move closer and closer to a
completely connected state, the cyclomatic number increases. The limitation of
the cyclomatic number arises since it depends upon the number of vertices and
edges only.
2.
Centrality within a Network:
D. Koning has developed an index known as Koning Number
for describing the degree of centrality of any node on a network. The koning
number for each node is calculated by adding up the number of arcs from each
other node using the shortest path available. For example, in Figure 4.7, point
D has the lowest number and is, therefore, the most central node in the
network.
3. Spread
and Diameter of Networks:
Kansky has developed two useful indices to measure the
diameter and spread of a network. These are Pi (π) index and Eta (η) index.
Pi
Index (π):
Kansky (1963) has developed Pi index (π) for the analysis
of transport network when the focus of inquiry is to investigate the
relationship between the transportation network as a whole and its diameter.
The ratio between the length of the network and the length of the networks
diameter would always be a real number, analogous to π. Therefore, the π index
may be written as:
π= total distance of network/ distance of diameter
Or
π=c/d
where c = total mileage of a given transport network
d=diameter
The application of π index to transportation network
would give a numerical value which would be greater than or equal to one.
Higher numerical values will be ascribed to more complicated networks and it
would reflect higher degree of development of the network.
Eta Index
(n):
The eta index () is quite useful when some spatial
characteristic of the network are under examination. This is also indicative
of spread of a network. The eta index (n) is given by the formula:
Η = total network distance/ number of arcs
or
η= M/E
where M = total network length in kms
E = the observed number of edges
Because the numerator is measured in kilometers,
therefore, the ratio is not scale free but represents the average length of an
edge of the network. This index is useful in examining the utility of a given
transport network. Kansky (1953) has used this index in analyzing the transport
network data for a number of countries.
4.
Detours:
The straight routes between two places or direct routes
(also known as ‘desire line’) are the routes, which travelers used to follow
because of their shortest distance. But straight routes are, however, seldom to
be found in reality; even the most direct route in practice deviates from
straight line. This type of deflection is very common due to physical
obstacles. Such deviations can be measured by the detour index where:
Detour index= actual route distance/ straight line
distance × 100/1
In other words, the detour index is the actual journey
distance calculated as a percentage of the desire line distance. In fact, the
actual route distance is almost always longer than the desire line distance,
then the detour index will be greater, in almost all cases, than 100 and in the
nature of things can never be less than 100. It is obvious that lower the
detour index, the more direct is a given route. The detour index is used for
assessing the effects which the addition or abstraction of links produce in a
given network.
Accessibility:
One of the most important attributes of a transportation
network relates to accessibility, and the geographer is particularly concerned
with accessibility as a locational feature. (Robinson and Bamford, 1978: 78).
When examining a transportation network, a geographer is also interested in
node-linkage associations in terms of accessibility.
The structure of a network, changes in response to the
addition of new linkages or the improvement of existing linkages. These changes
are reflected in changes in nodal accessibility. The measurement of nodal
accessibility is based on graph theory.





Comments
Post a Comment